
How we teach - a playful introduction to algorithms
This demo was created to show how we help 4-7 year old kids learn about algorithms and basic concepts of coding in a playful way.
Research findings show that children who learn coding at a very early age have more developed logic skills and a better grasp of cause and effect. Also, they are more persistent, confident, creative, and better at problem-solving than their peers. They often experience that if they set out to solve a challenge in a systematic way, and take it step by step monitoring themselves, their efforts will bring success.
This is the reason we think it is very important to have such a program accessible to children all over the world, not just ones from the Scandinavian education.
Let’s start!
We are going to tell you the story of 5-year-old Tomi, who took part in the testing of this program. We highlight one exercise for each logic section, but in the actual learning plan you will find some 15-20 ideas for activities and games to deepen the child’s understanding of the given section, not to mention the worksheets.
Now let’s actually begin!
At the beginning of the program, we put the following table in front of Tomi. Yes, this board was indeed made up of four egg holders. While developing the program, we ourselves were surprised at how many different things in the household we could use to make a board. The main thing is that each pit inside the egg holders marks a field on the board.

As you can see, some fields have got candies (borrowed from Tomi’s mum’s sweets stash), some fields are covered in lava (red balls), these are to be avoided.
Tomi must move the LEGO pirate to collect the candies while avoiding the lava fields. As some extra motivation, he could eat the sweets if he got them with the pirate. He had to use the following set of characters to control the pirate.
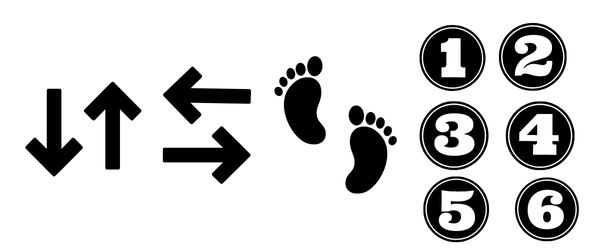
With the arrows he determined the direction in which the pirate was facing, the step signs meant moving forwards, and with the numbers he could say how many steps he wanted to take at a time.
So, on the first try, it took half an hour to work out the following algorithm. Of course, Tomi didn’t know he had to “write” an algorithm; the term was never actually mentioned during the program.
If you think it was easy, you are wrong. Quite a lot of adult help was needed in that half an hour, and at one point Tomi wanted to play something else because he hadn’t had much success in his first few attempts. Also, this one code sequence had only resulted in obtaining a single piece of candy. At that moment, it seemed completely impossible for Tomi to make up a code eight times longer than that and guide the pirate figure through the candy fields.
BUT we were very happy about this because our hypothesis was that this task would be too difficult at first for a 5-year-old child. We planned this task for after completing two thirds of the program, and the game with Tomi proved that for 4-7 year olds, the basic games and learning activities are needed for making up algorithms of this complexity.
So, we began building those foundations…
Basics
According to our curriculum, work on algorithms only begins on week 8, when we have laid the foundations for logical thinking about algorithms. Let’s take a step-by-step, week-by-week look at what we’ve learned with Tommy!
SEQUENCING
Within algorithms, operations usually have a defined order, so it is important that we make this rule clear for the child. Therefore, during the first week, we practise the order of operations through a variety of games and activities.
One of the ways to do this is to mix up the scenes of well-known stories and then arrange them in order. Tomi’s brother was in a school play last year called The Frog King, so that was one of the stories we broke down into parts. Here we made illustrations for the scenes, but for some other stories Tomi drew the details, and some we just discussed verbally.

The task here was to put the scenes in order within the story. In case you don’t know, the story is not about the princess disliking the prince and kissing him until he turns into a frog.
SYNTHESIS
This refers to the process of breaking down an operation into smaller manageable steps. There are two kinds of people: those who are scared off by a high school math equation and those who are not. Those who are scared see the equation as one whole and for them the task is solving the equation. Those who are not scared see several subproblems. They see that to solve the equation, they need to do a simple division, then a simple subtraction, then a simple multiplication, then another division, and finally an addition.
Everyone can add, multiply and divide, so they know that there is no need to be frightened by the equation. If everyone could see the smaller steps, probably far fewer people would be scared by equations. The problem is that we are usually not very good at breaking down tasks into sub-tasks.
The goal of this week was to make Tomi good at this. Good problem solvers are better than the rest at that one major thing: they can break down tasks into smaller steps.
That is what Tommy needs to learn, so that when he instructs the pirate, he doesn’t try to pick up all the sweets at once (that’s too difficult), but first to just go for the nearest one, then the one nearest to that, and so on.
For this we used activities instead of frogs and princesses, we talked about (and did) everyday activities. Vacuuming, tooth-brushing, washing the dishes. Activities that Tomi already knew well, but perhaps hadn’t thought about in such detail.
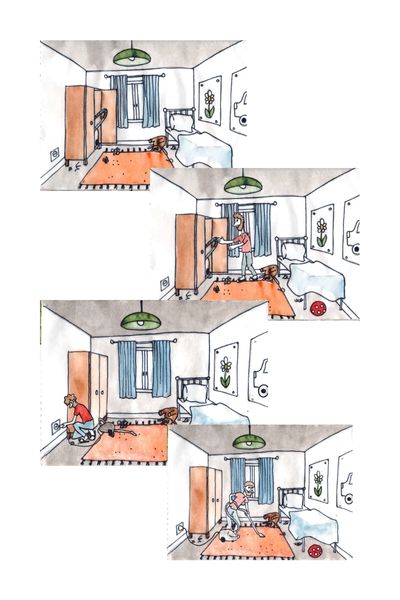
We made illustrations for these everyday activities too, so we could mix up the order and Tomi could put them back into the original order.
For the first two activity sheets, we made enough illustrations to make a whole storybook. We drew them by hand and digitised them afterwards.

BRANCHING
Just like in life and in computer science, most algorithms contain operations that are conditional. If it rains, we carry an umbrella. If it’s cold, we take a coat. If it’s Saturday, we sleep till noon (those who do).
In computing, for example, on Facebook, you can only see what I post IF you are my Facebook friend. On the egg board, you can only move the pirate to a field if it’s not covered by LAVA. So, Tommy must follow this logic to succeed with the pirate.
This is perhaps the ‘lesson’ for which we have devised the most games and exercises. There are virtually infinite possibilities. Every sorting exercise, every ‘if…, then…’ type of a challenge is a good way to practice this.
Our favourite was when we put tights on Tomi’s head with a tennis ball inside. We set up little half litre bottles and big coke bottles. His task was to tip the big bottles up like a bulldozer would but leave the small bottles standing.
BRANCHING AGAIN
We have dedicated an extra week to the topic of conditionality checking because we believe it is incredibly important. For this second week, we made things a bit more complicated, as there were no A and B cases, but several possible cases.
There can be cases A and B and C. Or you can have A, B, C, D, E, F, G and H. There can be so many possible cases that we don’t even know the number of all possibilities. A good example is a given train station, where I have no idea what trains stop. The one thing I do know is that I must board the train that goes to my hometown and stay on the platform while all other trains are arriving.
We used a lot of coloring and circling exercises. Perhaps the simplest was when Tomi had to color 3 different shapes in 3 different colors.

BUILDING BLOCKS
There are some operations that we know so well, do so routinely, that they have a name of their own. In computer science, we talk about this when a programmer writes a function and uses its name to refer to it later. There is no need to rewrite operations within the function, just to type in the name of the function and the computer knows what needs to happen.
In everyday life, this is what getting to kindergarten is like. We don’t list the motions of getting into the car, turning left, going to the main road, turning right, going to Sesame Street, turning off there, etc. Instead, we just say we are going to the kindergarten.
The best way to teach Tomi about this was through everyday activities. For example, we learned to bread chicken (popular thing to do in Hungarian kitchen). At first, breading was still a serious operation with three plates, one with flour, one with eggs and one with breadcrumbs. Plus, we had a fourth plate to collect the ready-to-cook meats.
Then he got the gist of it and the next week, the recipe no longer included all these steps, but referred to it simply as breading. And Tomi knew what to do.
LOOPS
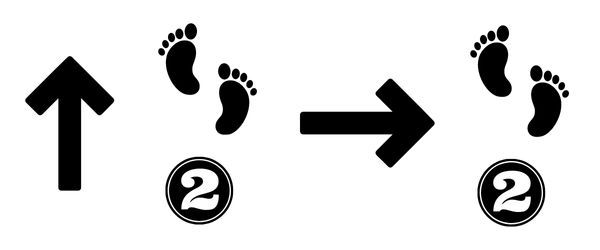
Loops are when an operation or a block of operations is repeated. It can also be a case where we have a specific number of iterations. This is what Tomi needs to give the pirate when he wants him to move forward by, say, three steps.
But there are also cases where we must repeat an operation until some condition is met. For example, to bread the meat until you have used up all the meat. Or keep moving forward until you hit a wall.
We have devised some very good coloring exercises for this.
DEBUGGING
In IT, this means finding the mistake. But in fact, in any kind of problem-solving, it is an advantage to be able to systematically check yourself and your work. Tomi needed this too, because he found it much easier to control the pirate once he started checking the code he had made. He noticed when the pirate missed candy or when he stepped on lava.
To practise this, naturally we used some classic cuckoo’s egg exercises. Perhaps the most memorable was when Tomi had to look for the fault in his parents’ outfits. Tomi’s dad had put on something that belonged to Tomi’s mom, and vice versa, and the child had to find the bug in the outfit.
The family shared a lot of laughter, so it was a great success for us too.
FOLLOWING ALGORITHMS
At this point in the program, we get to the algorithms. Tomi is not writing them yet; we are just following the instructions. First, we follow instructions in human language, then we learn about character sets where arrows and other images and icons convey the instructions.
By the end of the week, Tomi could read these ‘commands’ beautifully. Instead of an egg tray, this time we drew the track in the garden with chalk on the concrete. Dad wrote the instructions with the character set and Tomi had to translate this for his ‘robot’ Mum. So Mum was the robot, controlled by Tomi. But he didn’t write the instructions, he just helped the robot to interpret them.
PIRATING AGAIN
After all that, we used the egg holder again with the candies, the lava-filled fields, and the pirate. Tomi was already familiar with the character set, having successfully guided his mum with it on several occasions.
The use of loops was not a problem either and the number of steps was handled cleverly. He broke the task down into sub-operations, so he was always trying to navigate the pirate only to the nearest candy. This made the task seem more human, more transparent, and simple.
Avoiding lava fields, he cleverly collected the candies 8 weeks after the first failed attempt.

What’s next?
We still have 3-4 weeks left of the program and countless ideas on how to further complicate the problems Tomi can solve. Countless possibilities to expand the character set, introduce new types of obstacles and so on.
We can only really share the events of the last few weeks with those who join us, but broadly speaking, what has happened is that we have presented Tomi with increasingly complex, story-based challenges. And he wrote increasingly complex algorithms and solved them cleverly.
We hope you’re inspired to join our 12-week program. If so, click on the link. You can find all the information you need there.
